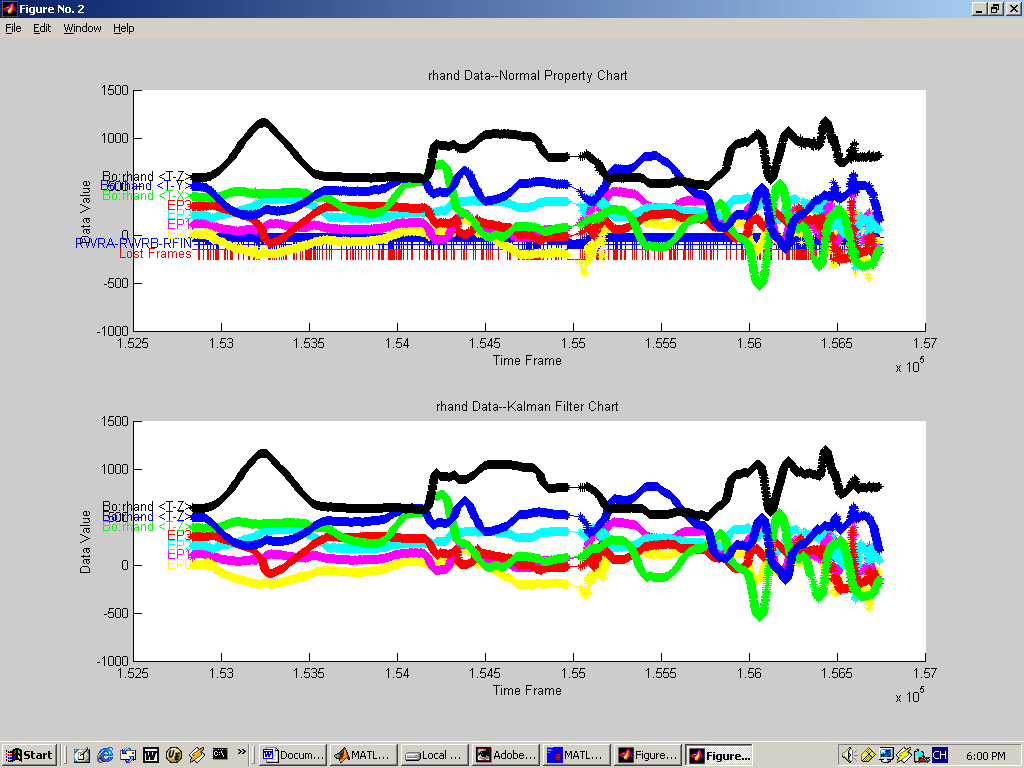
|
 |
||||||||||
| back | |||||||||||
|
Error AnalysisDirect error reasons:1.
Lose frames Reason: 1) Miss synchronization between real-time server and Lithtech engine while recording the data. 2) It cost the real-time server extra time to calculate one frame (position, rotation), thus delay the delivering time. Result: 1) No frame information available->all variables (position, rotation) keep stable -> the action freezes. 2.
Markers invisible (all/any) Reason: 1. The Vicon system cannot see the markers o Position out of range o Hidden markers 2. The Vicon system cannot label the markers o Fast actions o See more than actual markers Result: 1) Uncertain data generated from remaining visible markers 2) Uncertain data generated from springs attached on the skeleton 3.
Markers mislabeled Reason: 1. The Vicon system gets confused o Fast actions o Sudden actions 2. Some markers are invisible Result: 1) Error data of specific body 2) Impact on the whole object Typical error & Kalman filter performance1. Data
flipping o Position & Rotation (fig. ErrorJump.gif) 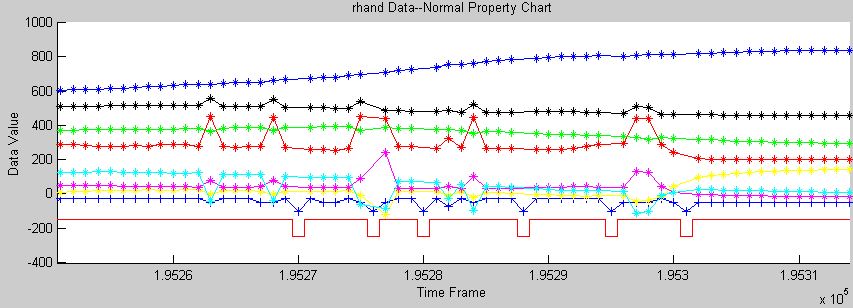
o Rotation
(fig. ErrorFlip.gif) 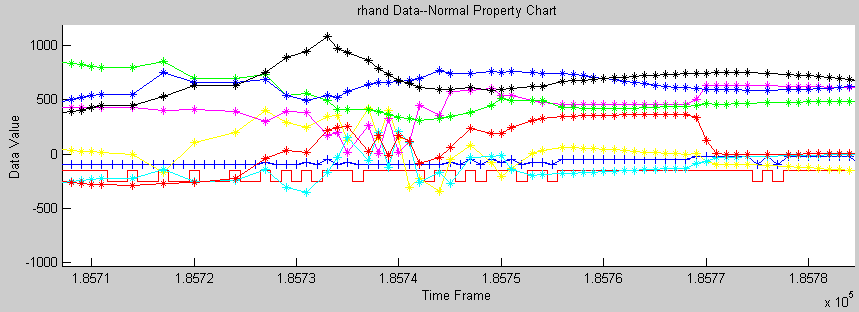
Solution:
Kalman Filter does a great job on such kind of error 2. Data
jump after a long frame-losing period o Position (fig. ErrorLong_pos.gif) 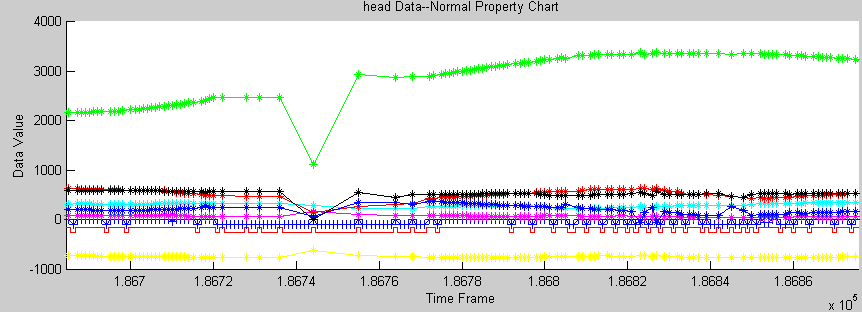
o Rotation
(fig. ErrorLong_angle.gif)) 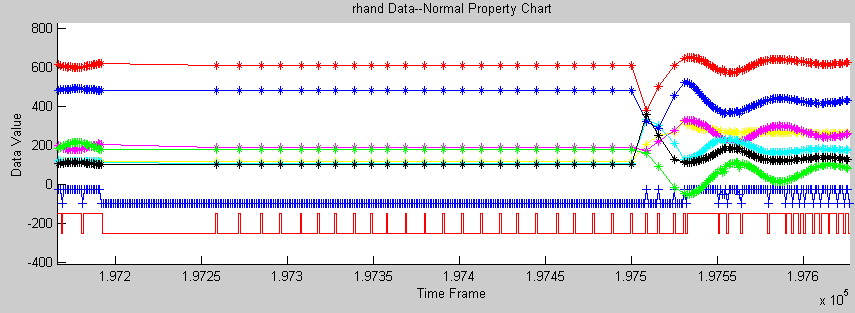
Solution:
Delete/correct wrong data by adding some latency (Wait to make sure) 3. Data
change when no/seldom markers visible o Position (fig. ErrorNoMarkerVisible_pos.gif) 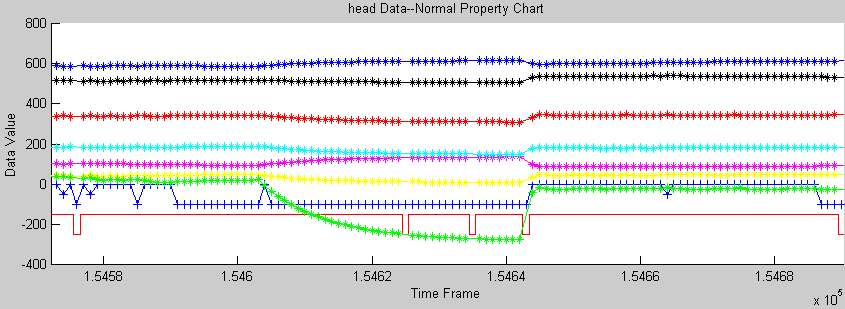
o Rotation (fig. ErrorNoMarkerVisible_angle.gif) 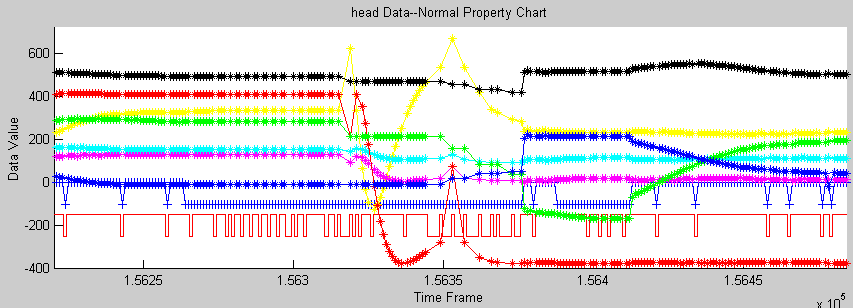
Solution: Combine the previous two solutions 4. Chaos
Data (fig. ErrorChaos.gif)
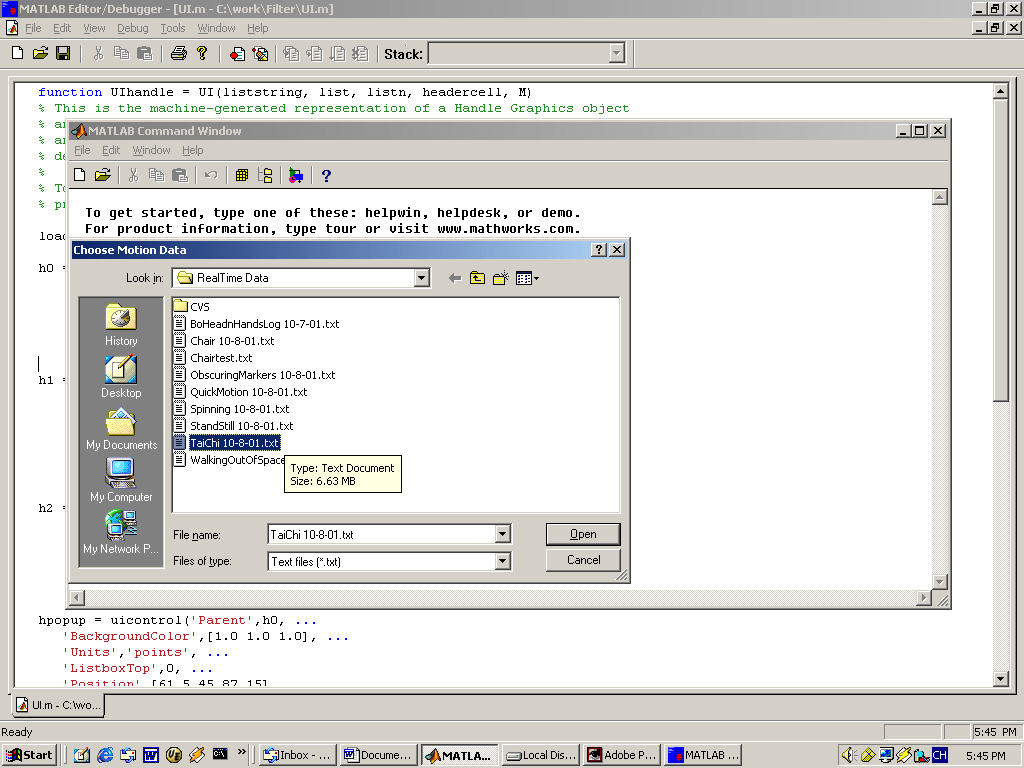
Solution: Combine the previous two solutions Mocap Data Analysis &Filter Research Program1. Interface Outlook (fig. ChooseFile.gif, UIBox1.gif, UIBox2.gif)
2.
Read in Mocap data stored in delimited text
format 3.
Automatically categorize data o Marker: position (P-X, P-Y, P-Z) o Body: Position (T-X, T-Y, T-Z) Rotation (A-X, A-Y, A-Z) Marker set 4.
Transform rotation data: o Angle-Axis -> Quaternion o Choose right Quaternion vector (Q or 每Q) to make the curve continuous 5.
Do filter process Current method: Kalman Filter 6.
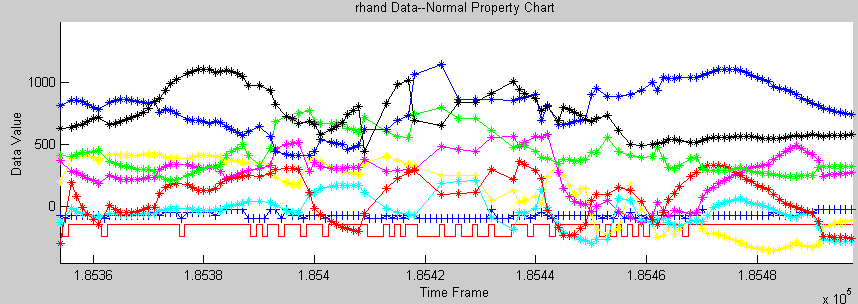
Plot original and filtered data (fig. PlotVariables.gif) o Position: T-X, T-Y, T-Z o Rotation in Quaternion: e0, e1, e2, e3 o Marker set (marker names, visible marker number) o Lost frame number 7.
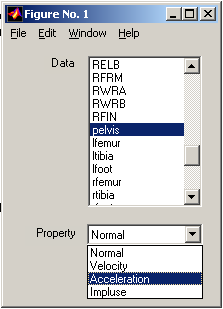
Show different properties of the data o Original o Velocity o Acceleration o Impulse 8.
Zoom Ability o Plots zoom in and out freely (fig. UIPlot.gif)
o Two plots zoom in/out the same position and scale 9.
Output filtered data in delimited text format Filter ResearchRotation Representation1. Common
rotation representation in Computer Graphics o Angle-Axis o Matrices o Euler Angle o (Unit) Quaternion/Euler Parameters 2. Q
& A Q: Why is that important for us? A: We need to find a good representation for rotation that can present meaningful, exact, continuous data curve for analysis and interpolation Q: Why use Quaternion? A: Advantage o The Quaternion space has the same topology and geometry as the set of rotations o Simple extrinsic equation (Angle-Axis <-> Quaternion) o Easy interpolation by using SLERP (Spherical Linear Interpolation) Disadvantageo Its 2-1 nature (Two Quaternion (Q, -Q) represent the same rotation) necessitates a preprocessing step Kalman Filter1. What
is Kalman filter? o The
Kalman filter is an optimal recursive data processing algorithm o Best possible estimator for a large class of problems and a very effective and useful estimator for an even larger class. 2. Target
System o General Kalman filter 每 Stochastic Linear system with Gaussian noise o Extended Kalman filter (EKF), Unscented Kalman filter (UKF) 每 Stochastic non-linear system with Gaussian noise 3. It
WORKS!!! Future Plan1. Delete/correct
wrong data by adding some latency (Wait to make sure) 2. Use
EKF or UKF instead of general Kalman filter 3. Filter
Parameters and tuning o System noise covariance o Measurement noise covariance o Mathematical model o Initial
state and covariance 4. Dual
Quaternions representation Reference﹞ Kalman Filter [1]
An
Introduction to the Kalman Filter Gary Bishop; Greg Welch ACM SIGGRAPH 2001 course [2] Chapter 1, Stochastic Models, Estimation, and Control, Peter Maybeck Peter Maybeck Volume 1, Academic Press, Inc [3]
The square-root unscented Kalman filter for state and
parameter-estimation [4]
The unscented Kalman filter for nonlinear estimation
[5]
Pose and Motion Estimation Using Dual Quaternion-Based Extended
Kalman Filtering J.S. Goddarda and M.A. Abidib Kevin Murphy, 1999 [7]
Sequential
Monte Carlo Methods Homepage Nando de
Freitas ﹞
Quaternion [8]
Smooth
interpolation of rotational motions Roberts,
K.S.; Bishop, G.; Ganapathy, S.K. [9]
Smooth Interpolation of Orientations With Angular Velocity
Constraints Using Quaternions Alan H.B.; Bena C.; Steven,
G.; John F.H [10]
Recursive
Methods for the Estimation of Rotation Quaternions August W.Rihaczek [11]
Using Quaternions
to Represent Rotation [12]
A Proof of
the Quaternion Rotation Representation [13] The Matrix and Quaternions
FAQ ﹞
Motion Capture [14]
A Real-Time
Anatomical Converter for Human Motion Capture T. Molet, R. Boulic, D. Thalmann [15]
Kwon3D Motion Analysis
Web Young-Hoo Kwon, 1998- [16]
Motion
-- Feature-Based, Long Range, Motion and Structure Estimates, Surveillance [17]
A Real Time Anatomical Converter For Human Motion Capture Tom Molet, Ronan Boulic,
Daniel Thalmann [18]
Motion Balance Filtering Seyoon Tak, Oh-young Song,
and Hyeong-Seok Ko [19]
Real-time
human motion analysis and IK-based human figure control
|
|
OVERVIEW
| YIN | YANG | THE
LAB
ENTERTAINMENT TECHNOLOGY CENTER
(c) 2001